COURBES COORDONNEES

Nous nous intéressons ici aux oscillations de trois systèmes de coordonnées courbes. Quand on examine de près une courbe dessinée, elle n'apparaît pas posée sur la surface du papier, mais possède une convexité ou une concavité relative par rapport à l'observateur, sans toutefois être absolues - elles peuvent être inversées en dessinant simplement les lignes correctes et on peut voir comment certaines formations hésitent entre l'intérieur ou l'extérieur.

"Pour que l'on puisse percevoir cette ordonnance de rythme en termes graphiques sous forme d' une pulsation intérieure et extérieure, il doit exister au coeur même des éléments, une sorte d'état d'équilibre instable. Des exemples familiers de ce genre d'équilibre se trouvent dans la fluctuation du voltage du courant alternatif, dans le balancement d'un pendule entre deux pôles de repos manifeste, dans la vibration d'une corde tendue. Un exemple de cet effet dans la représentation graphique, comme le comportement des courbes dans la gravure, a attiré notre attention. 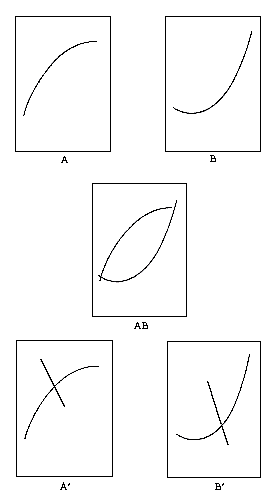Certaines sortes de courbes ne peuvent pas être vues comme posées à plat à la surface du papier sur lequel elles sont dessinées ou imprimées, mais sont tout de suite apréhendées par le spectateur comme étant convexes ou concaves. Remarquez dans le dessin (fig.VIII, A et B) la courbe A' perçue comme convexe et la courbe B' perçue comme concave.
A la différence des directions évoquées précédemment, ces configurations ne sont pas irrévocables. Un simple dispositif montré dans le dessin (fig.VIII, A'et B') consistant à tracer une ligne plus épaisse pour croiser celle qui se présentait comme convexe, la fera paraître concave et la ligne interrompue qui semble passer derrière celle qui était perçue comme concave, l'a fait paraître convexe. Dans des systèmes de courbes plus complexes, une troisième possibilité a quelquefois surgi: dans certaines circonstances, une ambiguïté concrète de positionnement peut apparaître, (Fig.VIII AB). A un moment donné, on voit ici une position concave-convexe; une seconde plus tard, elle devient convexe-concave. Dans les deux cas, c' est parfaitement clair et concret pour le spectateur. De tels phénomènes, connus depuis longtemps, se réfèrent souvent à des illusions optiques, distinctes des faits réels. Il va sans dire que comme nous nous occupons de ce qui est perçu par l'oeil, cette "illusion", dont la perception est universelle, représente tout ce dont nous avons besoin." 5
Ceci a une plus grande application par rapport à la théorie de la relativité en Physiques, où ces coordonnés courbes pourraient  être prises pour représenter les coordonnés non-Euclydiens d'une sorte d'espace déformé. Retournez voir les dessins exécutés à main levée de Hayter.(.III.,.IV.,.V.,.VI.)

.VIII. Dessin montrant des courbes perçues ou comme concaves ou comme convexes. S.W. Hayter
'Orientation, Direction, Cheirality, Velocity and Rhythm,The Nature and Art of Motion' , edité par Gyorgy Kepes. Studio Vista, Londres et New York, 1965, pp. 71-80, figure 8

Celles-ci engendrent des oscillations qui peuvent être développées ensuite avec de la couleur, tantôt chaude et qui avance, tantôt froide et qui recule, soit en choisissant soit en augmentant l'instabilité d'une manière ou d'une autre.
On peut regarder AB soit comme un tout emprisonnant l'intérieur d'une surface comme une bordure (presque comme un oeil) ou bien on peut le voir en deux sections distinctes enserrant la surface.
A' La ligne épaisse oblige, ici, la forme courbe à reculer et à se comporter comme une ligne frontière. C'est même plus évident si on prolonge la courbe, montrant ainsi l' orientation de sa ligne frontière.
B' La ligne interrompue contraint, dans ce cas, la courbe à passer au-dessus, et ce, comme une ligne frontière dirigée vers le haut.

Nous nous intéressons ici à la troisième dimension inhérente aux courbes, qui peut transformer une ligne a priori convexe en une ligne concave, cela dépend des courbes voisines. Il réside ici une ambiguïté systématique qui s' expliquera par l'idée que ces courbes agissent en réalité comme des coordonnées d' un système à trois dimensions voire plus.
'Systèmes tri-linéaires avec coordonnées courbes. Une ambiguïté surgit ici dans la mesure où les trois courbes conduisant à un système ouvert, doivent ployer dans la même direction, puisque, si la courbure est inversée, un système fermé se révèle. Il apparaît aussitôt que, si un couple de courbes quelconques dessine une surface convexe, alors la troisième courbe paraîtra toujours inversée donc concave. Afin de poursuivre la recherche dans plus de dimensions apparentes, on peut essayer d'employer la même structure avec quatre axes voire plus, dans lesquels, si nous considérons le convexe comme positif et le concave comme négatif, on peut étudier d'intéressantes double négations, des situations négatives par rapport à un axe et positives par rapport à un autre. Il va de soi qu'une telle recherche s'adresse aux membres pourvus d'une formation plus ou moins mathématique qui pourraient être enclins à continuer ensuite, avec des tirages à la fois digitaux et analogiques, réalisés par ordinateur.'

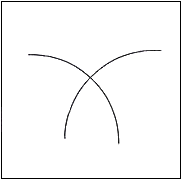
Fig.54. Intersection de deux courbes
Intersection de deux courbes concaves qui s'ouvrent dans la même direction de telle sorte qu'elles n'auront aucune tendance à se chevaucher. On peut imaginer sur celles-ci des axes coordonnés possédant la même forme fondamentale. C'est un système ouvert.

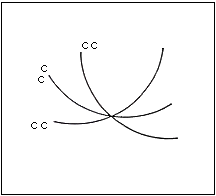
Fig.55. Intersection de trois courbes convexe, convexe, convexe
Intersection de trois courbes convexes qui constituent un système ouvert. On peut imaginer chacune d'entre elles comme un axe coordonné.

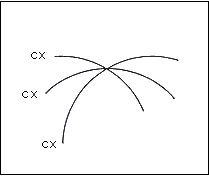
Fig.56. Intersection de trois courbes se déployant vers le bas, convexe, convexe et convexe
Celles-ci représentent un système ouvert sans possibilité de chevauchement.

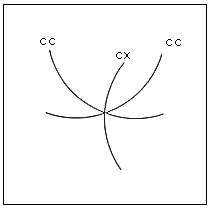
Fig.57. Intersections de trois courbes concave, concave et convexe
Ceci montre ici comment deux systèmes concaves forcent le troisième (fondamentalement neutre) à paraître convexe. C'est un système fermé.

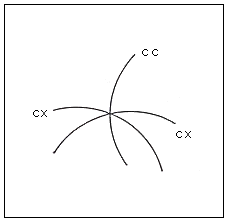
Fig.58. Intersection de trois courbes convexe, convexe et concave
Nous avons un exemple ici de la façon dont deux systèmes convexes obligent la même courbe précédente à paraître concave.

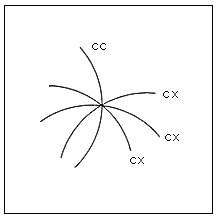
Fig.59. Intersection de quatre courbes convexe, convexe, convexe et concave
Ceci peut former une surface plate banale mais quand on imagine ces courbes prolongées dans la troisième dimension pour former des champs, on obtient une impression ambiguë de leur appararition et dispararition (voir figure 48).

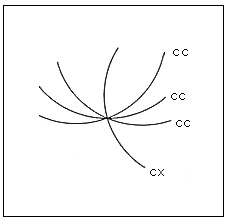
Fig.60. Intersection de quatre courbes concave, concave, concave et convexe
Ceci peut former une surface plate banale mais quand on imagine ces courbes prolongées dans la troisième dimension pour former des champs, on voit des espaces jonglant à l'intérieur de manière ambiguë.

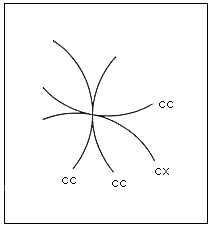
Fig.61. Intersection de quatre courbes convexe, concave, concave et concave
Après les figures suggérant de quelque manière que ce soit, trois dimensions ou plus avec ambiguïté, des motifs simplement plats semblent ressurgir. Après un certain degré de complexité, on retourne, semble-t-il, à une figure en deux dimensions.

Notes sur les applications possibles à la cosmologie

Dans un sens plus large, ces distinctions entre convexe et concave pourraient être appliquées à la cosmologie. Si l'on considère ces courbes comme des coordonnées dans l'espace, il est possible selon leur courbure, de distinguer deux modèles dans l'univers. L'un suggère l'utilisation de la théorie de la relativité d'Einstein - courbée, définie mais illimitée - quelque chose comme les (quatre dimensions) surfaces d' une balle de foot. Il aurait une courbure positive et continue.
L' autre suggestion constitue un autre système de cosmologie. Tout système ayant deux convexités et une concavité ou une convexité et deux concavités seraient fondamentalement différents, conduisant à la représentation de la surface d'une selle de cheval qui fit l'objet d'une hypothèse, contemporaine en fait avec celle d'Einstein, par le physicien hollandais De Sitta. Son modèle était le premier à préfigurer l'univers en expansion comme découvert plus tard par Hubble. Utilisées sous cette forme, leurs possibilités confèrent une densité et une concrétisation aux ambiguïtés dont il est question ici.

5  S.W. Hayter, 'Orientation, Direction, Cheirality, Velocity and Rhythm.The Nature and Art of Motion' (édité par Gyorgy Kepes). Studio Vista, Londres et New York, 1965, pp. 71-80, figure 8

sommaire

retour