TWO CONTINUOUS TRACES
Here the interaction of convergent and
rectilinear systems is investigated to clarify how the convergent systems leave their
imprint in the resultant lines even when they have been removed.
'Commencing with the simplest three line systems (x,y,z rectangular coordinates) laid out
with pencil on a sheet, an erratic trace is followed using alternate x, y, z directions
starting from an edge and returning to the margin at another point but carefully avoiding
the point of convergence. A second trace playing against the first will emphasize this
effect.'

.B. Rectangular coordinates system. Drawing
executed with a computer
One has found in carrying this out with a computer that an extraordinary phenomenon arises
by itself - namely that the space of the coordinate system curves around the center of the
convergence - a mathematical reflexion of Einstein's idea that space is curved around
matter.
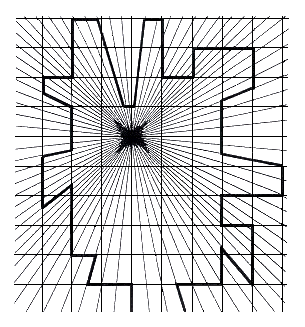
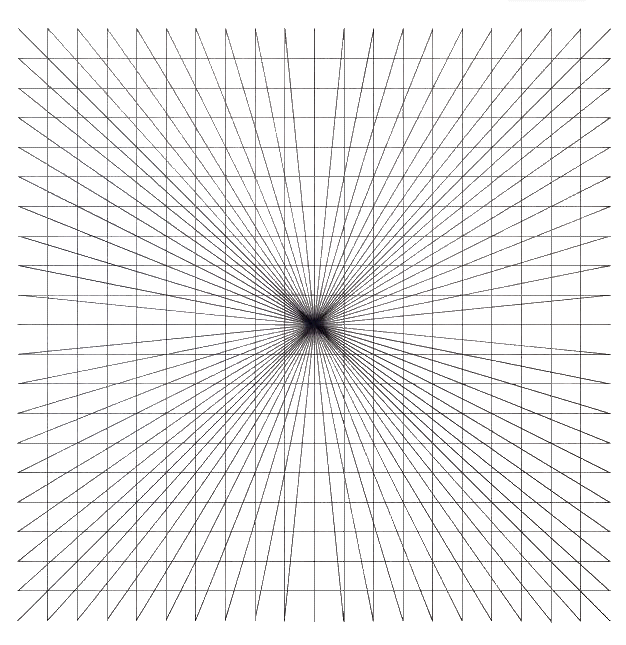
Fig.62. One trace on a convergent axis and
vertical and horizontal parallels
One continuous trace is made at random among the convergent system and the rectilinear
system to give a heightened impression of centripetal forces acting on them both.This is
stronger because they are interconnected within these systems.
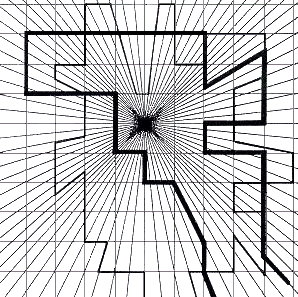
Fig.63. Two traces arising on a convergent axis and horizontal and vertical parallels.
Fig.64. Two traces extracted from figure 63
These two traces extracted from their coordinate systems provide an even stronger
impression of being acted upon by centripetal force.
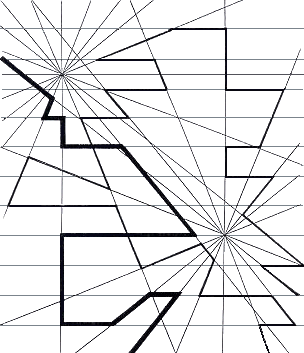
Fig.65. Two continuous traces on two
convergent axes and horizontal parallels
The two continuous traces are constructed at random following sections of the two
converging systems and sections of parallel lines to give an impression of a strong
irregular attraction.
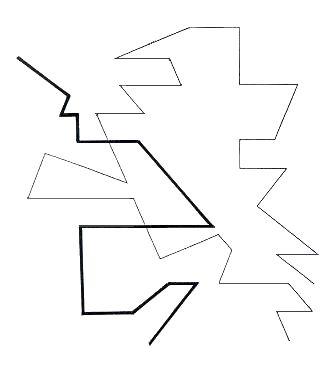
Fig.66. The two traces extracted from figure
65
These two traces extracted from the two converging and parallel systems exhibit an
attraction to the powerful centripetal forces mitigated by some parallel travelling.
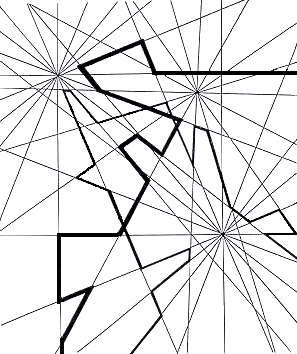
Fig.67. Two traces on three convergent axes
Two continuous traces made at random among the converging systems give an almost violent
impression of centripetal forces at odds with one another.
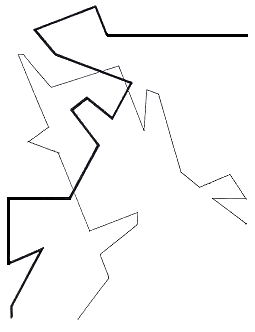
Fig.68. The two traces extracted from figure
67
Two continuous traces extracted from their coordinate systems give a violent impression of
competing attractive forces unmitigated by any parallel paths. These two continuous traces
extracted from the framework of three converging systems suggest a number of centripetal
centres acting (each partially determined by each) in a way that leads up to the situation
of deterministic chaos.
In fact according to the laws of perspective, the single point of view is made for a
single observer and he must be at a precise position to enjoy it. It is solipsistic. If
there are more observers, each from his own point of view can enjoy another vanishing
point and when he moves, the vanishing point moves with him. This is illustrated here with
three vanishing points and one can see the interaction between them. However, it can be
much more sophisticated as illustrated by the computer diagrams of fractals and systematic
chaos, which had begun to interest Hayter toward the end of his life, in which an infinity
of vanishing points, all articulated with reference to all of the others, is presented.
This is a subtle interaction of all of the individual vanishing points with the whole.

Image n°1. Computer representation of
Deterministic Chaos 1
"Nr. 22/85",ESTHETIQUE DU CHAOS, Palais de la Découverte,1989 Paris, Germany
In this representation we can see a great number of vanishing points, but in an
enlargement even more could actually be seen. One can go on and on enlarging and
perceiving more vanishing points up to the point of the computer's resolution ability;
this is an arbitrary given which could be improved. One can never in principle reach the
final number which is a denumerable infinity, like the infinity of natural numbers.

Image n°2. Computer representation
of Deterministic Chaos 2
"Nr. 22/85",ESTHETIQUE DU CHAOS, Palais de la Découverte, 1989 Paris,
Germany
This is an enlargement of Image n°1, wherein one can perceive many more vanishing
points. This is an unfinished process rather than a definite counting.
back |