STRAIGHT-LINE AND CURVED-LINE SYSTEMS (SIGMOID AND HELICAL AXES)

Here straight line systems have been expanded to include curved lines - convex, concave and curvilinear - which interact with straight line systems and with each other. Our drawings have been augmented with some of Hayter's own, drawn free hand, exhibiting his understanding of how subtle curves can function.
'Elaboration of the two-element systems using straight lines/convex curves; straight lines/concave curves; convex/ concave curves; concave/convex curves; convex/convex curves; concave/concave curves---'

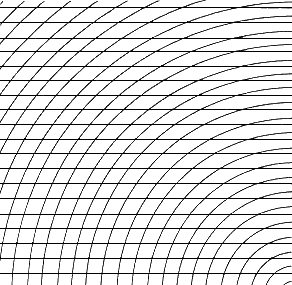
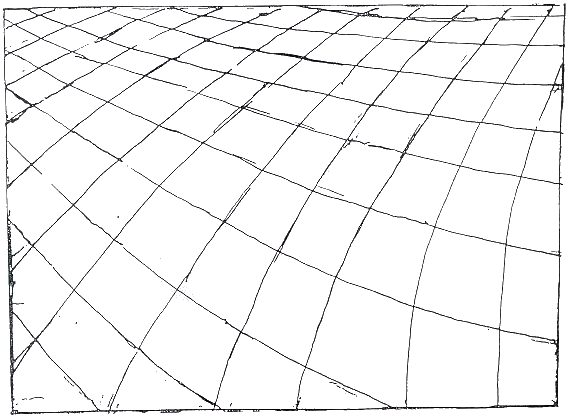
Fig.26. Horizontal parallels superimposed on convex curves
The convex curves interact with the straight parallels creating an optical phenomenon resulting in nodes (points at rest in a vibrating body) which arise in the lower right hand corner. They might give rise to a field for the operation of unconscious drawing.

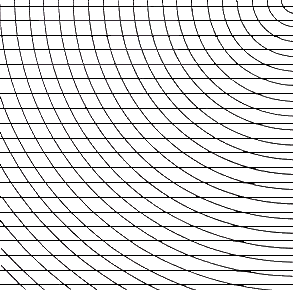
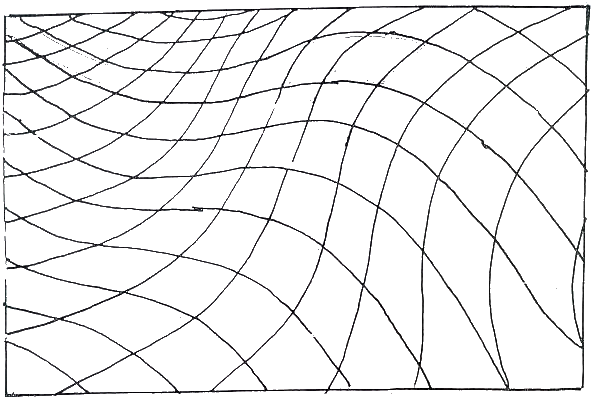
Fig.27. Horizontal parallels superimposed on concave curves
Here the interference patterns which will be investigated thoroughly in section 'Interference, Vibration, Moires' begin to assert themselves.

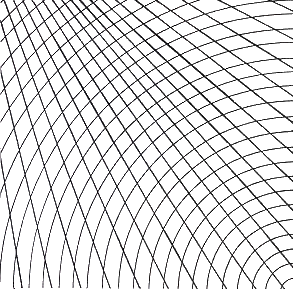
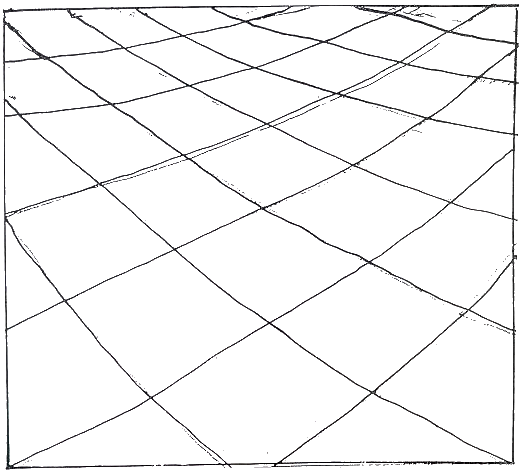
Fig.28. Divergent system arising outside of the picture plane superimposed on convex curves
These form a coherent field which one might develop further through unconscious drawing.

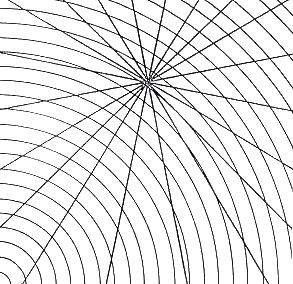
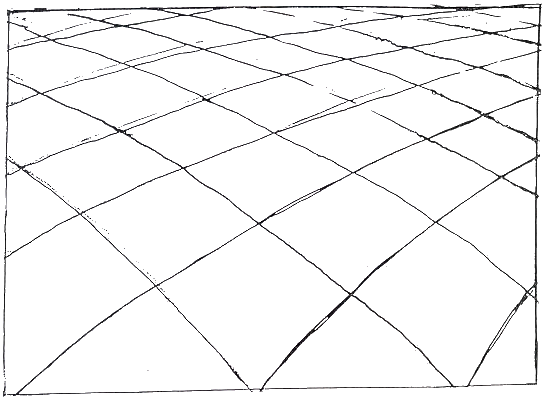
Fig.29. Convergent system superimposed on convex curves
The convergent centre articulates these curves as contracting from the lower left but expanding from the upper right.

The exposition continues beyond the apparent curvature established by straight lines to real curvature. There are a number of intersecting curves drawn precisely and by Hayter himself free hand. These twisted spaces can form essential elements in paintings as well as embodying ideas similar to those used by Einstein in twisted spaces (Riemannian and Lobachesky geometries) in theories of relativity. It is possible to use these curved spaces in setting up a field and drawing unconsciously (see section 'Unconscious Drawing') into it, the drawing being controlled in some mysterious but precise way by the complex spaces suggested. Here is a real fusion of ideas from science and art.

.III. CONVEX - CONCAVE, S.W. Hayter
Free hand drawing, 'New Ways of gravure', 1981, New-York, Watson-Guptill Publications.
These curves are convex diverging from the outside upper left and concave parting from the upper top right. This complexity creates an impression of a cosmic space and of the world seen from outside and above.

.IV. CONCAVE - CONCAVE, S.W. Hayter
Free hand drawing, 'New Ways of gravure', 1981, New-York, Watson-Guptill Publications
These concave curves are diverging out of the upper right and upper left hand edges. They might present a field in a view through a microscope.

.V. CONVEX - CONVEX, S.W. Hayter
Free hand drawing, 'New Ways of gravure', 1981, New-York, Watson-Guptill Publications
These convex curves issue from the lower right and lower left hand corner. One might fruitfully undertake an unconscious drawing in space.

.VI. CONCAVE - CONVEX/CONVEX - CONCAVE,S.W. Hayter
Free hand drawing, 'New Ways of gravure', 1981, New-York, Watson-Guptill Publications
This is complex, changing from concave/concave in the upper right hand corner through twisting lines to convex/convex on the upper left side. It contains, as do all of these hand drawn diagrams, a suggestion of a Einsteinian map of space being twisted by matter.
These all make the hand-drawn diagrams more precise but do not incorporate their gradual divergence.

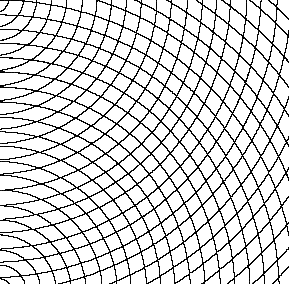
Fig.30. Concave curves superimposed on convex curves

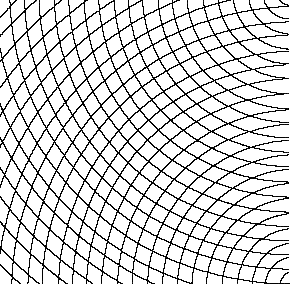
Fig.31. Convex curves superimposed on concave curves
(Here the interference patterns which will be investigated thoroughly in section 'Interference, Vibration, Moires' begin to assert themselves tentatively, twisting the eyes, appearing and disappearing.)

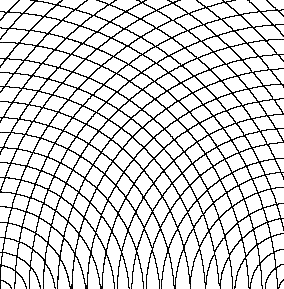
Fig.32. Convex curves superimposed on convex curves

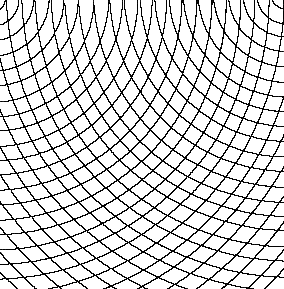
Fig.33. Concave curves superimposed on concave curves
In all of these one can see the beginning of moiré patterns which will be further explored in section 'Interference, Vibration, Moires'. Curvilinear forms are introduced here.

'---/continuing with sigmoid axes, helical axes---'

Fig.34. Parallel horizontals superimposed on curvilinear forms
These create a vibrant, oscillating space which is convincing in itself but might be exiting when used as a basis for unconscious drawing.

Fig.35. Concave curves superimposed on curvilinear forms

Fig.36. Diagonal sigmoid curves superimposed on convex curves

Fig.37. Asymmetric helical axis

Fig.38. Asymmetric helical axis superimposed on divergent system arising outside of the picture plane
This asymmetric helical axis demonstrates a violent convergence into a deeper centre.

Fig.39. Asymmetric helical axis superimposed on concave curves
This asymmetric helical axis causes the concave system to expand to the left and converges to the right.

.A.Two asymmetrical helical axes (computer drawn) are placed within range to influence each other deeply

home

back