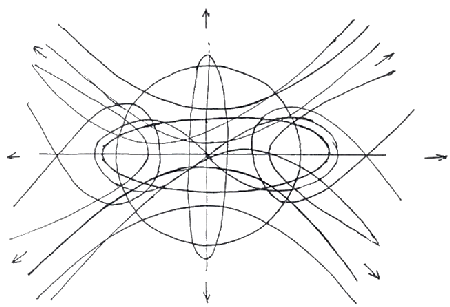
"Counterpoint is a term we have borrowed from music to indicate a consequent but not always rational relation. The simple mechanical consequences of an ellipse are demonstrated and it is made clear that this is not an invention on our part but an effect existent in nature and accessible to anyone sufficiently alert."⁷
The ellipse is fundamental because it is a more generalised form of which the circle is a specific instance (having an equidistant radius at all points) and it suggests all of the forms incorporating curves - parabolas etc. However these curves are drawn mechanically, they illustrate the kind of curves used in the visual equivalent of counterpoint - the inversions, progressions and deformations.

.XXIII. MECHANICAL COUNTERPOINT, S.W. Hayter
'New Ways of Gravure', S.W. Hayter, New York 1981, Watson-Guptill Publications.

An extension to the exposition is continued with what might be called a visual mechanical counterpoint to a group of forms derived from a circle. But what has counterpoint to do with mechanics? - Are they not completely opposed? - Counterpoint which refers especially to music is an art of superimposing melodic lines on a given melody according to fixed but somewhat fluid rules. Whereas mechanical refers to a machine, levers or wheels, inclined planes and screws, it might explain phenomena by means of mechanical action. They both suggest a certain rigidity but seem at first sight irrelevant.

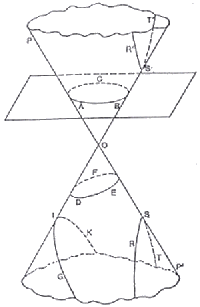
Fig.157. A number of the curves below are derived from conic sections: A circle from the horizontal section of the cone itself. Ellipse results as a section taken at an angle. A parabola arises as the straight section through the cone - its conic edges acting as asymptotes with which the parabola coincides only at infinity and

a hyperbola which keeps slightly curving inward never even at infinity reaching the lines cut through the cone. All of these have an algebraic formula to the power of two,

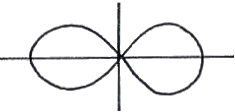
whereas the figure of eight (a lemniscate) is quartic.

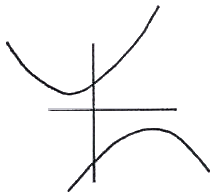
Then there is the catenary chain, curves which were superimposed on parabolas to show their similarities and differences.
So one has a great number of curves either springing out from the centre or being attracted to it.

⁷ 'New Ways of Gravure', S.W. Hayter, New York, Watson-Guptill Publications, 1981