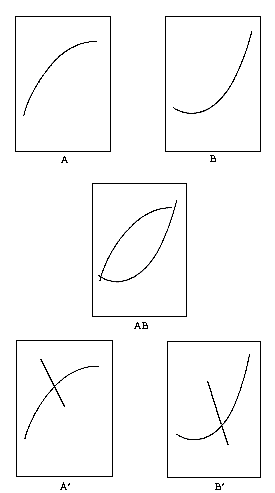
CURVED COORDINATES

Here we consider the oscillations of three curved coordinate systems. When one inspects a drawn curve, it does not appear to lie on the surface but has a convexity or a concavity relative to the observer but these are not absolute - they can be reversed by simply drawing the right lines and certain formations can be seen as fluctuating in and out.

"For this order of rhythm to be seen in graphic terms as an in-and-out pulsation, there must exist in the elements themselves a certain state of labile equilibrium. Examples of this sort of equilibrium are familiar to us in the fluctuation of potential in alternating current, in the swing of a pendulum between two extremes of apparent rest, in the vibration of a stretched cord. One case of this effect in graphic representation was brought to our notice in the behavior of curves in engraving. Certain types of curves cannot be seen as lying on the surface on which they are drawn or printed, but are immediately understood as being convex or concave to the observer.Notice in the diagram (Fig.VIII, A and B) the curve A seen as convex and B as concave. Unlike those orientations referred to earlier, these configurations are not absolute. A simple device shown in the diagram (Fig.VIII, A' and B') of placing a stronger line to intersect that which appeared to be convex will cause it to appear concave, and the interrupted line which appears to pass behind the curve which was seen as concave, has made it appear convex. In more complex systems of curves a third possibility has sometimes been found to arise: in certain circumstances a concrete ambiguity of position can appear (Fig.VIII, AB). Here one sees a concave-convex position at one moment; a moment later it becomes convex-concave. In both cases this is perfectly clear and concrete to the observer. Such effects, which have long been known, are often referred to as optical illusions, as distinct from matters of fact. Needless to say, as we are dealing with that which is perceived by the eye, that "illusion" which is universally seen is all the fact that we need." ⁵
This has a much vaster application in relation to the physics of relativity where these curved coordinates might be taken to represent non-Euclidian coordinates of some twisted space. Look back at Hayter's free hand drawings, (III,IV,V,VI)

.VIII. Diagram showing the perception of curves as concave or convex. S.W. Hayter
'Orientation, Direction, Cheirality, Velocity and Rhythm. The Nature and Art of Motion' (edited by Gyorgy Kepes). Studio Vista, London and New York, 1965, pp. 71-80, fig 8

These establish oscillations which can be further developed with colour, either warm and advancing or cool and receding, either deciding the lability one way or the other or emphasising it. (see section 'Colour-Transparency'). AB can be seen either as a whole enclosing the inside area as a limit (almost like eye) or it can be seen in two separate sections bounding the area. A' Here the heavy line markes the curved form to recede and function as a boundary. This is even more evident if one extends the curve, showing the directions of its boundary. B' Here the interrupted line forces the curve above and as a boundary directed upward.

Here we deal with the third dimension implicit in curves which can transform a seemingly convex line into a concave depending on the neighbouring curves. There is a systematic ambiguity here which will be explained by the idea that these curves function in reality as the coordinates of a three or 'more' dimensional system.
'Three-line systems with curved coordinates; here an ambiguity appears as the three curves leading to an open system must be curved in the same direction for if the curvature is inverted a closed system is projected. This immediately appears as if any two curves demonstrate a convex surface whereupon the third will always appear inverted as concave. To continue research into further apparent dimensions the same structure may be attempted with four or more axes in which if we are able to consider convex as plus and concave as minus some interesting double negatives, situations negative to one axis and positive to another, can be investigated. It is clear that such research will be confined to those members of a more or less mathematical formation who might be disposed to continue further with computer printouts both analogical and digital.'

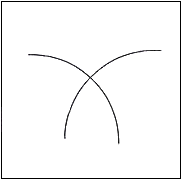
Fig.54. Intersection of two curves
Intersection of two concave curves which open in the same direction so they will have no tendency to overlap. On these, coordinate axes can be imagined - having the same fundamental shape. It is an open system.

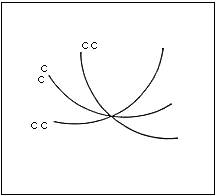
Fig.55. Intersection of 3 curves convex, convex, convex
Intersection of three convex curves which constitute an open system. One can image each of these as a coordinate axis.

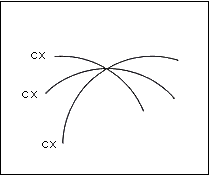
Fig.56. Intersection of three curves opening downward, convex, convex and convex
These too represent an open system with no occasion to overlap.

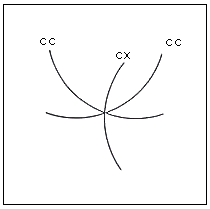
Fig.57. Intersection of three curves concave, concave and convex
Here this is an example of how two concave systems force the third (fundamentally neutral) to appear convex. This is a closed system.

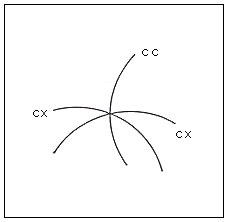
Fig.58. Intersection of three curves convex, convex, and concave
Here we have an example of how two convex systems oblige the same curve to appear as concave.

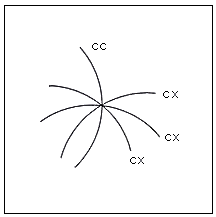
Fig.59. Intersection of four curves convex, convex, convex and concave
This can form a banal flat surface but when these curves have been imaginatively completed in the third dimension to form fields, one gets an ambiguous impression of their appearing and disappearing.(see figure 48)

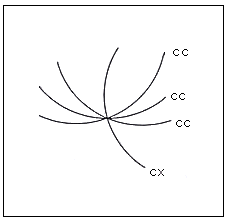
Fig.60. Intersection of four curves concave, concave, concave and convex
This can form a banal flat surface but when these curves have been imaginatively completed in the third dimension to form fields, one sees spaces within ambiguously juggling.

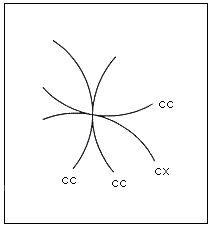
Fig.61. Intersection of four curves convex, concave, concave and concave
It seems here that after figures suggesting, however, ambiguously three or more dimensions of space, one returns to mere flat patterns. It seems that after a certain degree of complexity one returns to a figure in two dimensions.

Notes on the possible applications to cosmology

In a vaster sense, these distinctions between convex and concave might be applied to cosmology. If one regards these curves as the coordinates in space, it is possible through their curvatures to distinguish two models of the universe. The one suggests Einstein's use in relativity: - curved, finite but unbounded - somewhat like the (four-dimensional) surfaces of a football. It would have a continuous positive curvature. The other suggestion is another system of cosmology. Any system having two convexities and one concavity or one convexity and two concavities would be fundamentally different, leading to a representation of the surface of a saddle, which was actually hypothesized simultaneously with Einstein by the Dutch physicist, de Sitta. His model was the first to prefigure the expanding universe as discovered later by Hubble. The possibility of these being so used lends a density and concreteness to the ambiguities here discussed.

⁵  S.W. Hayter 'Orientation, Direction, Cheirality, Velocity and Rhythm. The Nature and Art of Motion' (edited by Gyorgy Kepes). Studio Vista, London and New York, 1965, pp. 71-80, fig 8.

home

back