STRAIGHT-LINE SYSTEMS, CURVED AXES AND HELICOID CURVES

'Continuation of similar experiments using three line systems as x, y, z continued with curved axes not necessarily circular and with helicoid curves.'

Fig.40.Superposition of 3 diverging systems arising outside of the picture plane
Linear systems are shown distorting the space - causing it to oscillate toward the left then determinedly toward the right - a version of the optical illusion of the double cube which oscillates decisively forward or backward.

Fig.41. Two divergent systems superimposed on parallel horizontals
This seems to create a flat pattern of triangles but on looking upward toward the right and downward from the left an oscillation appears.This figure seems to create a pattern rather than an illusion of space whereas the ones following create more space, being curved and so fitting into various Riemannian curved space geometries. Are these physically able to create the impression of four dimensions or does the eye oscillate between three perceived dimensions and other different three dimensions in a continuously labile motion?

The exposition continues with the extension to curved axes, the axes being repeated to form fields.

Fig.42. Two diverging systems superimposed on concave curves
This changes extraordinarily depending on where and how one looks, the curved part writhing with one and then the other diverging sections, the opposite one hovering above.

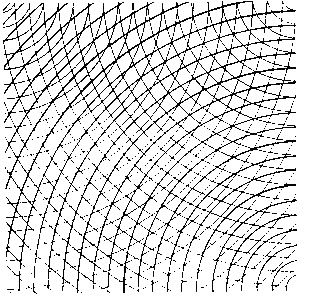
Fig.43. Concave curves superimposed on concave curves going in the opposite direction superimposed on convex curves
This oscillates in and outsidethe lower left corner andthe upper right but the central section remains locked as an overlapping pattern.

Fig.44. Diagonal curvilinear forms superimposed on concave curves superimposed on concave curves
The superimposition of the two concavities acts as a field. The diagonal curvilinear form, suggesting a direction of movement, oscillates with these fields causing giddiness.This creates an undulating space.

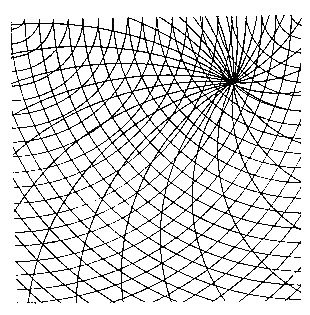
Fig.45. Asymmetric helical axis superimposed on concave curves superimposed on concave curves
The curves must pass through the helical axis becoming one field.This reads as a spatially deep field except in overlapping when the lines result in rigidity.

Fig.46. Diagonal curvilinear forms superimposed on convex curves superimposed on concave curves
This is the same as fig.44. but the direction of one curve has been changed from concave to convex. This too induces vertigo.

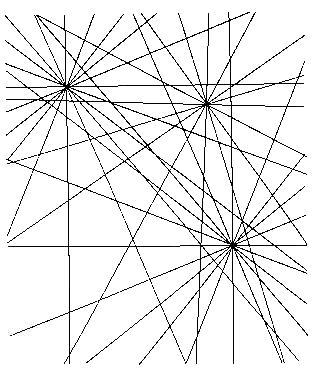
Fig.47. Three converging rectilinear axes
Consider how these three vanishing points within the same diagram meet and modify each other. If one obscures the actual vanishing points, there is violent oscillation in the surrounding area. (See this heightened on figures 65 and 66 - where the traces are being extracted from the converging systems). Can we modify the forms of intuition? Superimpose what at first sight seems too many fields to ascertain whether the eye can learn to respond to them all ambiguously, to see whether they create space or are perceived as flat, and whether, for a single observer, this perception changes with time.

Fig.48. Diagonal curvilinear forms superimposed on convex curves superimposed on concave curves superimposed on bow curves
In spite of the four dimensions here employed, one can see distorted space appearing and diappearing in an ambiguous way.

Fig.49. Diagonal curvilinear forms superimposed on convex curves superimposed on convex curves superimposed on convergent axis
The introduction of a straight-line coordinate system into this curved complex negates the oscillation. At what point does this complexity of dimensions become flat, a two dimensional interweaving of lines signifying nothing spatially deep?

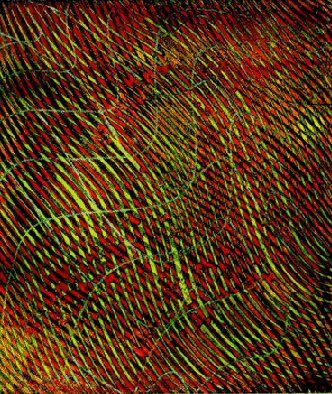
.VII. GREEN WAVE, S.W. Hayter
1965 (etching, 592 x 500 mm), Collection of Julian Hayter, 'Hayter e l'Atelier 17', Carla Esposito, Electa, Milan 1990, p.125
This flicks in and out as a pattern and as a suggestion of deep space and also acts by interference (see section 'Interference, Vibration, Moires').

The exposition continues by revealing how dots (in a physical sense, matter) can be apparently displaced by coordinate systems.
'---/ The purpose is to use these fields as operators: transformations of the space can be demonstrated by interchanging one field with another and sheets with a number of fixed points viewed in transparency over these systems show apparent displacement.'
There follows a number of such experiments in the apparent displacement of three dots by the superimposed fields. Riemannian complexities of space curved by the matter in it according to the theory of Einstein are important in exploring three-line curved systems and even four-line systems. Observe whether your eyes, after a time, can react ambiguously to four-line curved systems.

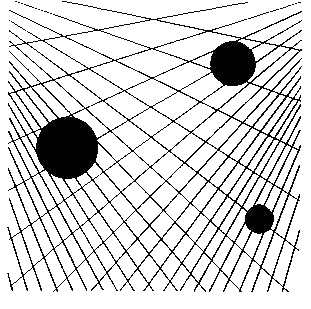
Fig.50. Three dots against two diverging systems
The three dots hover in space above two converging systems.

Fig.51. The same 3 dots against diagonal curvilinear forms superimposed on curves
The three dots from right to left seem to be sitting within, above and falling within the diagonal curves.

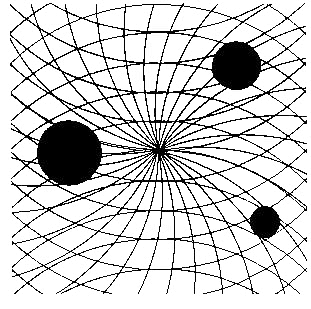
Fig.52. The same 3 dots against a helical axis superimposed on concave and convex curves

Fig.53. The same three dots against diagonal curvilinear forms superimposed on concave and convex curves
The three dots are suspended within this space.

home

back