
STRAIGHT-LINE DIVERGING AND CONVERGING AXES
The exposition continues with the meeting
of straight lines in converging and diverging systems - either converging inside or
outside of the picture plane. Although these lines are "in reality" straight,
they appear to be bent. This is not an optical illusion but an optical property. Some of
these oscillate from concave to convex and back again. A few of these are explored here.
'Further with straight line systems of two elements construct diagonal fields with
convergences as the conventional two point perspective leading to the apparent deformation
of the surface. It is interesting at this point to observe that if this is carried far
enough fields will appear convex and not flat.'

Fig.23. Two convergent systems.
Although the lines are actually straight, they appear to turn in and out - to be concave
(between the two vanishing points) and to be convex in the lower section. This occurs in
the perception itself. This is not an optical illusion. It is an optical reality.

Fig.24. Two diverging systems
The upper part of these figures seems convex (as if it were covered by cumulus clouds) and
the lower half concave.

Fig.25.a. One convergent system superimposed
on divergent system arising outside of the picture plane
This appears oscillating.
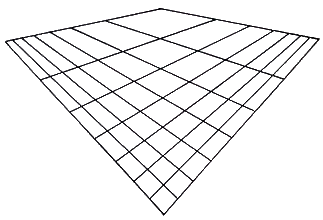
Fig.25.b. This arises, as does the similar fig 24, from the intersections of two diverging systems (bottom part only here illustrated). The surface so constructed seems to be deformed. Although constructed from rectilinear systems, it seems to be convex.
back |